Chasing Time: how fast can Python perform in single-thread computations?

Unfortunately, it's not that simple. There is no single law that operates the Universe, so there can be no single language that describes the Universe. Each programming language designed to solve a specific set of problems is very weak to other languages in some aspects. So, where does the end of application of one or another language lies? In search for answers, some programmers delve into interesting experiments. We will discuss one of such experiments below.

Valery Golenkov, a developer from Sibedge, has been developing applications in different programming languages for over 10 years. Once Valery's friend asked him to help with calculation of functions according to systems of equations to calculate data gathered over a specific period of time. It was part of a scientific project the friend was working on.  Valery decided to solve the problem using Python. According to IEEE Spectrum*, Python is the most popular language among programmers. It is also actively used for scientific computations in the Anaconda suite.

The systems of equations are as follows:

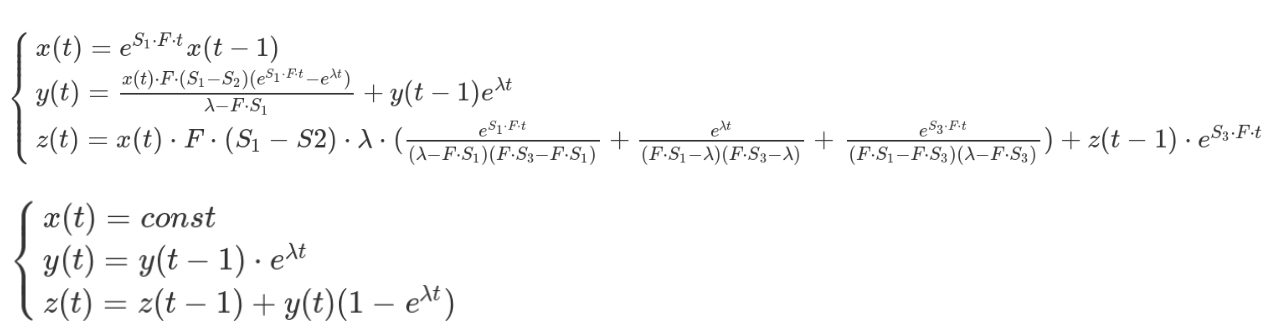
Try not to be scared by the complexity: even a beginner programmer can translate these formulas into code. However, there’s an “unforeseen consequence”, as the old saying goes: each subsequent function calculation depends on the previous one. This means that we won’t be able to run parallel processes and will have to perform sequential computations. The problem is further aggravated by the fact that function values have to be calculated for a time span of 10 days with a resolution of 1 nanosecond. Nuclear physics is not for weaklings, you see. 1 billion operations per second on four floating point values and 864 trillion operations overall.

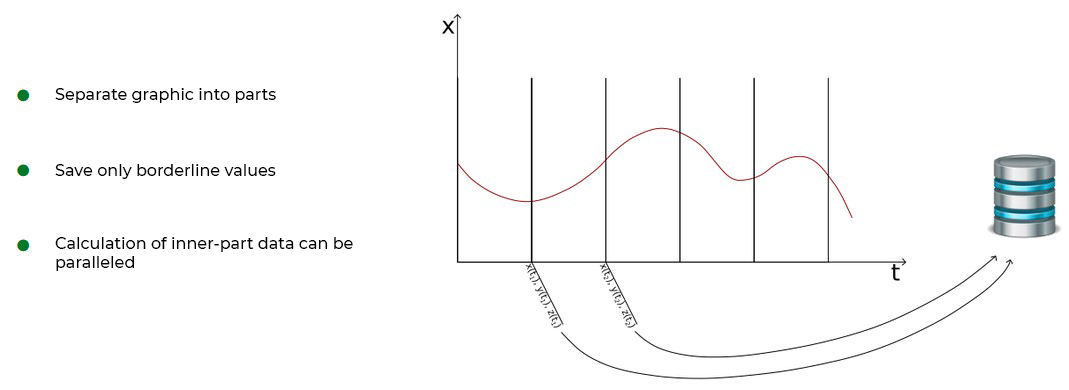
All these computations are required to visualize different time spans, which will make it possible for scientists to evaluate the system's behavior. There’s a burning issue: how do we avoid getting the DBMS flooded by the massive data stream? The solution quickly presented itself. Since systems interchange performing tasks, we can write only borderline values for the modes while calculating intermediate data on the fly. With this approach, we can partially parallelize the jobs, assigning certain time spans to threads.

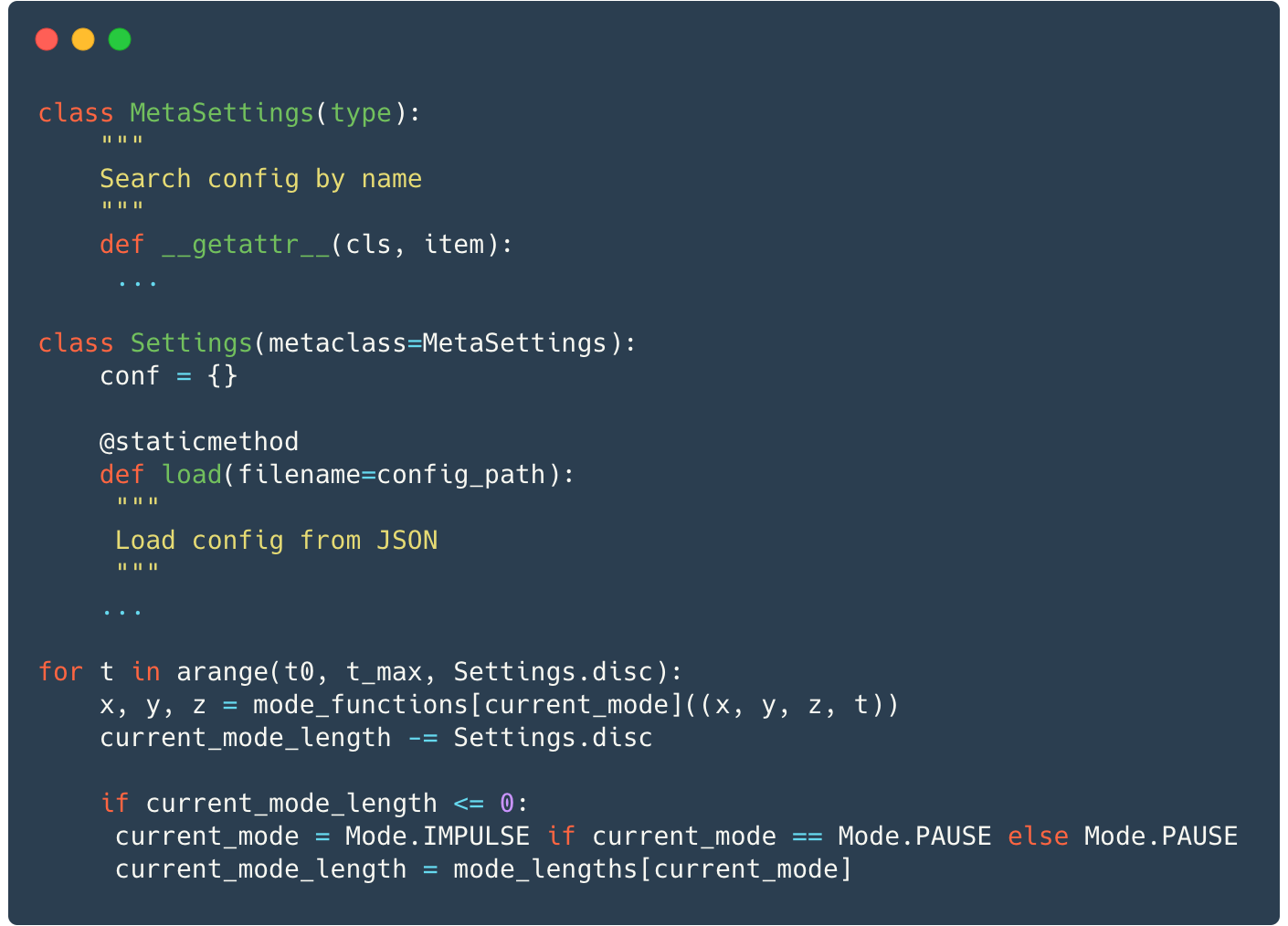
Walt Disney once said: “The way to get started is to quit talking and begin doing.” So, as the fist step toward a solution we made a draft build of the program to roughly evaluate the calculation time. In the draft build, we have implemented functions that describe the systems of equations (in the listing below, there is a fragment that calculates the second system). They receive four rational numbers (x, y, z, t) as input and they return three numbers (x, y, z).

We will store the initial function values, calculation times and other constants in JSON and we’ll load it at program start into a static field of the settings class using a static method. For convenience, let us create a metaclass to make it simpler to access the settings class fields. In the main function, let us create the main cycle with command variable mode. This variable will define for which system we calculate function values in this iteration. Functions are called from the main cycle as well. Piece of cake!

Our program performs great calculations but it's a bit slow. It took 338.197 seconds to make calculations for 0.1 seconds of data. It was a rude awakening for us to realize the project lead may not live to see the calculation results for 10 days of data. That’s because the calculations would take over 90 years. Inventing a time machine was not an option, so we embarked upon program optimization.

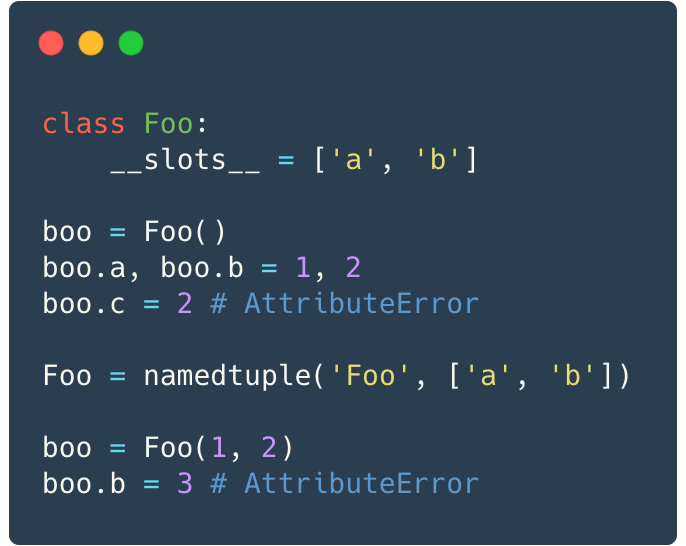
Let us tweak structures and algos. When you do blindfold programming, you normally consider structures from the point of view of how convenient it is to use them. In our case this translates into the modification of the class Settings with a metaclass to store all program settings. However, if you use Python and you need fast access to some settings, you’d better consider storing them separately in fast access structures. For example, you can store some constants for calculations in a namedtuple — immutable (read-only or unchangeable) container, or use a makeshift с __slots__ class as mutable (changeable, extendable). Here, the second option is better since __slots__ specifics have been developed to save memory space.

So, what is it? This is a static class field that stores the list of class parameters. It’s visually simple but complex inside. If a class has this field, then CPython places all the described class attributes into a fixed-size array that can be accessed much faster. The drawback of this approach is that you won’t be able to assign any other parameters to objects of this class. But performance is more important to us, in this case.

We are actively using class Settings in the functions to obtain calculation constants. Let us move all required constants to the namedtuple structure, which we’ll pass to functions as an argument instead of Settings class.

What do we get in the end? It now takes 215.005 seconds to make calculations for 0.1 seconds of data. This is only 58 years. We need to finish the experiments before retirement age comes around, so let us continue playing optimization. Did you actually think how often we make function calls? In CPython for each function call, the __call__ method of the function object is invoked, which consumes interpreter time. At each such call, the interpreter allocates a stack slot for arguments, defines function type and executes it, and then clears the stack. At a first glance, this set of routine operations does not look redundant. However, in our case this succession is executed with each cycle iteration, which translates into a huge overhead.

Let us cut the number of Python function calls in the cycles. To that end, let us move a part of the cycle into the functions: now each function performs calculations for multiple iterations (not for a single one) until values x, y and z need to be calculated for another system of equations. Since we try to decrease the volume of calculation data stored by writing only borderline values, it is sufficient for the functions to return the latest values.

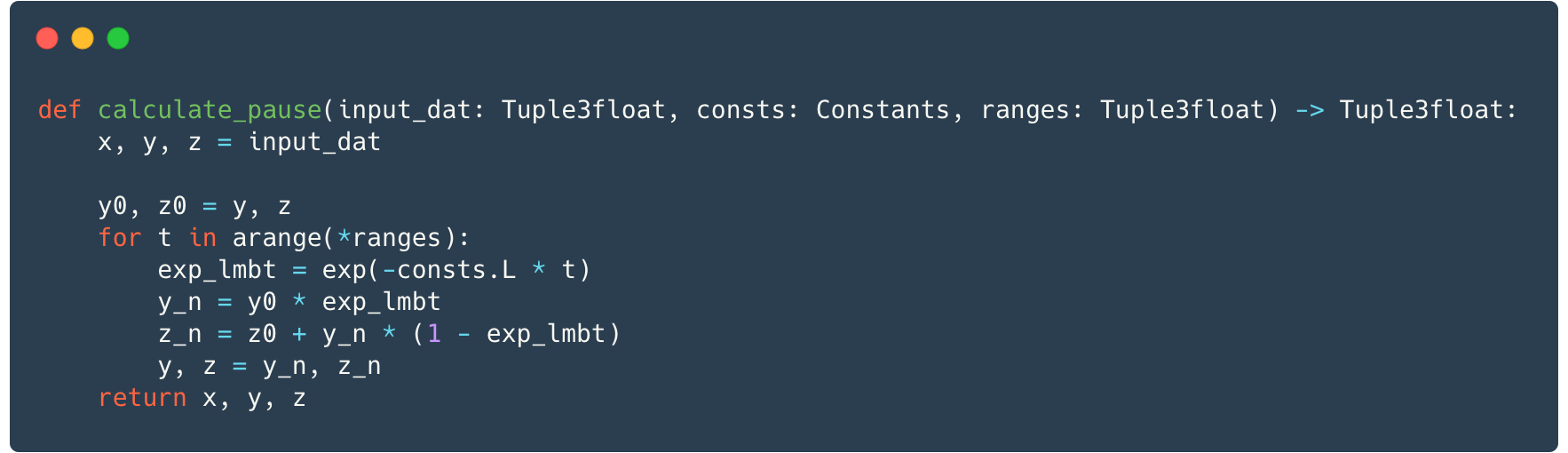
Hard to believe, but it now took 25.027 seconds to calculate 0.1 seconds of data! We’d have to wait for results for mere 7 years. However, with extra effort we could make even better optimizations.

Let us use one more trick. The use of namedtuple has yielded good results but that doesn’t mean there’s nothing left to optimize.  To gain extra performance, it makes sense to move namedtuple constants to local variables, because that removes one more mediation function (__getitem__) when accessing constants.

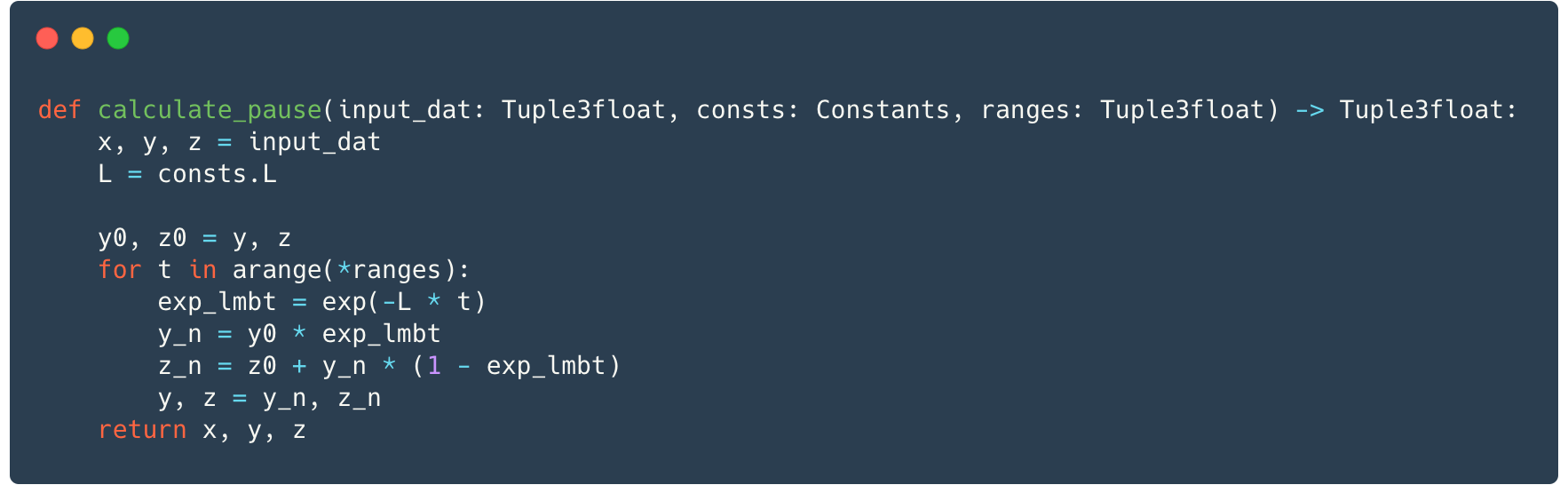
We see yet another performance improvement from 25.037 to 20.558 seconds. Of course, you may think 5 seconds is not that impressive as compared to proper call design from the previous optimization. However, for long calculations these 4 seconds may mean a day, two or even a year! Current optimization has reduced the calculation time down to 6 years!

Python is a language standard, and its specific implementations on C, Java and other languages comply with that standard. There’s even such exotic implementation as Python on Python or PyPy. It’s not an interpreter but a full-fledged JIT compiler, and some popular libraries and frameworks like NumPy, SQLAlchemy and Django have been ported from it. Since bytecode is compiled jnto machine code and then executed by a processor, it all works way faster than on CPython. Let us run our code on PyPy. What do we have now? It now takes 3.294 seconds to calculate 0.1 seconds of data! It will take less than 1 year to get the results.

If PyPy gives such a performance boost, why do developers not use it ubiquitously? There are two reasons for that. Firstly, there are many libraries that PyPy does not support. Secondly, there’s only a 32-bit compiler version for Windows and that means all runtime libraries have to be 32 bit.

Using all sorts of magic we managed to achieve outstanding results. Still, there’s one more trick up the sleeve to make it a lot faster. As funny as it sounds, this trick is writing the program in C++. This way, we are now able to calculate 0.1 seconds of data in mere 0.441 seconds, which translates to 44 days overall.

Let’s see what we have now. Optimizations have boosted performance by over 100 times. And still using low-level C++ has proven to be more efficient in our case. A rather obvious conclusion follows: Python is not suited for complex single-thread calculations. We need to always bear in mind the language’s scope of application and diligently select tools for solving specific problems. Optimizations and workarounds are a lot of fun. Still, you can invest your time and energy with better results